Dark green-copper Eye Look
This is for Jigyasa!! :-*

I’ll give the product suggestions first:
1. Foundation: Lakme Invisible Finish Foundation (Yes you read it right!!!) As Jigyasa has very nice skin and does not need much coverage, this is a nice, light water based foundation and only for Rs. 180/-. I use this one almost daily as a concealer and use compact on top. I don’t use foundation daily, and looking at your pics, you don’t need to invest in one.
2. Compact: Maybelline whitestay UV or Lakme ka naya waala. 😛 Rs. 150/-.
3. Green Eye pencil: Bourjois Khol and Contour Pencil or Maybelline Vivid and Smooth. (Please check if the maybelline one is waterline safe, as the Bourjois one is.) Both around Rs. 225/-.
4. Eye Shadow: Maybelline Chai Latte Quad. (It takes care of everything.) Rs. 225/-
5. Mascara: Maybelline Colossal Volume Express Rs. 350/- approx.
6. Eye lash Curler: Vega Rs. 100/-
7. Lipstick: Colorbar “Love that Rust” Rs. 250/-
8. Blush: Colorbar “Just Earth” Rs. 250/-
So let’s start with the look.
For the eyes:

1. Start by priming your lids.
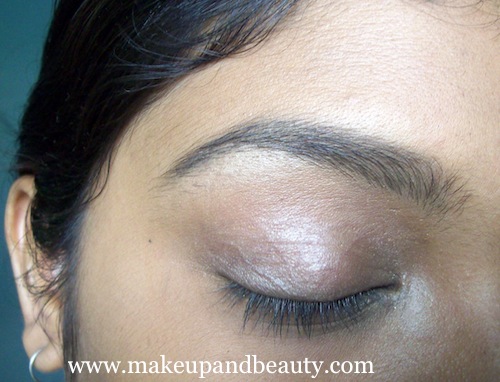
2. Take a dark green eye liner pencil (the one I have used here is a khaki one as I don’t have an emerald green pencil) and draw a thick line along the upper lash line. Take the line right into the crease and fill in the outer V.

3. Smudge the liner as shown below.
4. Apply a copper eye shadow (from the Chai Latte Quad) dead centre of your eye lid and blend well with the green liner.
5. Highlight your brow bone (Again from the Chai Latte Quad)

6. Use the same green liner to define your lash line. Wing out the liner a bit for added drama.
7. Curl your lashes and apply mascara.
DONE!!!!
Apply a maroon/rust/copper brown lipstick and the “just Earth” blush.
You can also add a fun twist to the messy bun you have planned.
Just section of some hair from the front of the larger part. Like so:
French braid the hair very loosely and add to the side ponytail.
Get the messy bun ready. Pull out a few strands from the braid to get the soft, messy romantic look.
All the best!!!
Love
Mrunmayee
Also Read :
Lotus Hypnotica Eye Contour Definer Photos, Swatches
Party Make Up Tutorial: Turquoise Blue/Green Eyes and Neon Pink Lips
Makeup Suggestion for Copper-Blue Saree : Ask IMBB
Copper & Brown Makeup Look Photo Tutorial
Eye Makeup Look using Lakme Glide on Eye Colour – Warm Copper
Copper Eye Makeup Tutorial
Easy 3-minute Neutral Eye Makeup Tutorial

















:inlove: :inlove: :inlove: :inlove: :inlove: :inlove: :inlove: :inlove: :inlove: :inlove: :inlove: :inlove: :inlove: :inlove: :inlove: :inlove: :inlove: :inlove: :inlove: :inlove: :inlove: :inlove: :inlove: :inlove: :inlove: :inlove: :inlove: :inlove: :inlove: :inlove:
Hehhehehehahahahahaa…I will copycat this look and patent and claim it as mine… :yahoo: :yahoo: :yahoo: :yahoo: :yahoo: :yahoo: :yahoo:
Please do!!! I’ll copy cat your vada recipe!!! Nobody will know!!! :secret2: :secret2: :secret2: :secret2: :secret2:
😐 😐 the vada will also look prettier…you might put dark green curry leaf liner for it :worship: :worship: :worship: :worship: :worship:
mrunnn me ecoppy catt tooo :yahoo: :yahoo: :yahoo: :yahoo: :yahoo: You totally rocking red lippy in this one.. :yahoo: :yahoo: :yahoo: :yahoo: :yahoo: :yahoo:
Rati..i was wondering..did u get a mail from me?!!
Thanks Ratidoo!!! Actually it’s the rust one we got free from Colorbar.. It’s showing up all Laal laal in the pics.. ?:) ?:) ?:) ?:) ?:)
bt it’s looking nice. 😀 😀 😀
Love it Mrunmrun!! 🙂 🙂 :yahoo: :yahoo: :yahoo: :yahoo: :rose: :rose:
Thankoo Pathu darling!!! :-* :-* :-* :-*
I am definitely gonna copy cat this…It looks soooooooooooooo rockkinggggggggggggg!!! :woot: :woot: :woot: :woot: :woot: :woot: Mrunnnn… :-* :-* :-* :-* :-* :-* :-* :-* :-* :-*
You are soo pretty Mrun!! :hypnotized: :hypnotized: :hypnotized: :hypnotized: Me staring!!!! staringggggggggggggg
Thankoo Cali!!!! You know. khoobsurati dekhnewale ki aankhon mein hoti hai, or something to that effect!!! :toothygrin: :toothygrin: :toothygrin: :thanks: :thanks: :thanks: :thanks:
me want to copyyyyy cat thisss look soo much now!! :toothygrin: :toothygrin: :toothygrin: :toothygrin: :toothygrin: :toothygrin: :toothygrin:
im gonna do the bun 😀 you simply rock in red lips :)) .. i cant dare to do that :worship: :worship:
Thanks Shreya!!! It’s the simplest, cutest hairdo.. :thanks: :thanks: :thanks: :thanks:
Loved your look and especially the hairstyle is super awesome :))
Thanks maha!!! :thanks: :thanks: :thanks:
luv it 🙂
Thanks Rids!! :toothygrin: :toothygrin: :toothygrin: :thanks:
:woot: :woot: :woot: :woot: :woot: :inlove: :inlove: :inlove: :-* :-* :-* me gonna try that hair style right now!!!!!!!!!!!! :happydance: U R THE BEST!!!!! :heart:
Please do Sireesha!! It would look even cuter on you!!! :thanks: :thanks: :thanks: :-* :-* :-* :-*
u r looking HHHHHHHOOOOOOOOOOOOOTTTTTTTTTTTT :waytogo:
Awww.. Thanks Sim!!! :blush: :blush: :blush: :thanks: :thanks:
ok..this is only for general awareness here 😛 –
” One interesting study showed that men on a somewhat dangerous bridge, when approached with a questionnaire by a pretty researcher who left them her phone number in case they wanted to know about the study she was conducting, were much more likely to phone and request a date than men who were relaxing on a park bench. Apparently, the risk, the danger, the level of arousal that resulted from this risk, was transferred to the female researcher causing her to appear more attractive and all of this decision stuff was outside of conscious awareness. “
Men are such adrenaline slaves!!! :yelo: :yelo: :yelo: :yelo:
:rose: :rose: :rose: :rose: :rose: :rose: :rose: :rose: :rose: :rose: :rose: :rose: :rose: :rose: :rose: :whistle: :whistle: :whistle: :whistle: :whistle: :whistle: :whistle: :whistle: :heart: :heart: :heart: :heart: :heart: :heart: :heart: :heart: :heart: :heart: :heart: :heart: :heart: :heart: :heart: :heart: :heart: :heart: :inlove: :inlove: :inlove: :inlove: :inlove: :inlove: :inlove: :inlove: :inlove: :inlove: :inlove: :inlove: :inlove: :inlove: :inlove: :inlove: :inlove: :inlove: :inlove: :inlove: Mrunnnnnnnnnnnnn!!!!!!!!!!!!!!!!!! saxyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyy :woot: :woot: :woot: :woot: :woot: :woot: :woot: :woot: :woot: :woot: :woot: :woot: :woot: :woot: :woot:
OMGG!!! :blush: :blush: :blush: :blush: :blush: :blush: :blush: :thanks: :thanks: :thanks: :thanks: :thanks:
Mrun :heart: :heart: :heart: :heart: :heart: :heart: :heart: :heart: :heart: :heart: you taking requests…..I will also send my request to you :happydance: :happydance: :happydance: :happydance: :happydance: :happydance: :happydance: :happydance:
you looking fab Mrun :heart: :heart: :heart: :heart:
JOmolaaaaaaaaaayyyyyyyyyyy happy bdayyyyyyyyyyyyyy :yelo: :yelo: :yelo: :yelo: :yelo: :yelo: :yelo: :yelo:
oye..its Jomol’s b’day today kya?? Happyyyyyyyyy B’dayyy Jomolll!! :joker: :joker: :joker: :joker: :joker: :joker: :joker: :joker: :joker: :joker: :joker: :joker: :joker: :joker: :joker: :joker: :joker: :joker: :joker: :joker: :joker: :joker: :joker: :joker: :joker: :joker: :joker: :joker: :joker: :joker: :joker: :joker: :joker: :joker: :joker: :joker: :joker: :joker: :joker: :joker: :joker: :joker: :joker: :joker: :joker: :joker: :joker: :joker: :joker: :joker: :joker: :joker: :jiggy1: :jiggy1: :jiggy1: :jiggy1: :jiggy1: :jiggy1: :jiggy1: :jiggy1: :jiggy1: :jiggy1: :jiggy1: :jiggy1: :jiggy1: :jiggy1: :jiggy1: :jiggy1: :jiggy1: :jiggy1: :jiggy1: :jiggy1: :jiggy1: :jiggy1: :jiggy1:
Hawwwwwwwww u didnt knw Cali..me and Rads hav even sent her a bouquet today…. :rose: :rose: :rose: :rose: :rose: :rose: :rose: :rose: :rose: :rose: :rose: :rose:
Hainn!!! I don’t believe you guys!! :smug: :smug: :smug: :smug: :lying: :lying: :lying: :lying: :lying: :lying: :lying:
Caliiiiiiiiii….sachchiiiiii :weep: :weep: :weep: :weep: :weep: :weep: :weep: :weep: u dnt trust us ask Rati :wilt: :wilt: :wilt: :wilt: :wilt: :wilt: :wilt: :wilt:
Farha’s failed attempt at making all of us April fools!!! :yelo: :yelo: :yelo: :yelo: :yelo: :yelo:
he he he Mrunn…me loouuuuuuu you!!! :-* :-* :-* :-* :-* :-* :-*
O:) O:) O:) O:) O:) O:)
many many happy return of this day jamol……….. :cake: :cheers: :party: :joker:
Thankoo Jomolaayyy!!!! You don’t need to send request, you can order for a look!!!! :-* :-* :-* :-* :-* :-* :-*
Mrun 😯 😯 😯 😯 :shout: :shout: :shout: :shout: :shout: :shout: :shout: …i wanted everyone to wish JOMO …kiti majja yenar hoti… :vampire: :vampire: :vampire: :vampire: :vampire: :vampire: :vampire: :vampire: :vampire:
Farha.. Whoops!!! Sorry sorry.. 😉 😉 😉 But that was ur plan na??? Ho na???
wow mrunmayee…
the hair dooozzzz loook lovely… :victory2: :victory2: :victory2: :victory2: :victory2: :victory2: :victory2: :victory2: :victory2: :victory2: :victory2: :victory2: :victory2: :victory2: :victory2: :victory2: :victory2: :victory2: :victory2:
Thanks a lot Noopur!! I will try, waise am not very good with hair… :thanks: :thanks: :thanks:
no no no… jomols happy birthday in on 2 may… 😐 😐 😐 😐 😐 😐 😐 😐
No noopur she didnt wanna be embarrassed thats y she didnt tell us here…its today only…wish her :rose: :rose: :rose: :rose: :rose: :rose: :toothygrin: :toothygrin: :toothygrin: :toothygrin: :toothygrin: :toothygrin: :toothygrin: :toothygrin:
hain ji????
jomol ne fb pe 2nd may likha hua hai happy bday….
?:) ?:) ?:) ?:) ?:) ?:) ?:) ?:) ?:) ?:) ?:)
ARIP FOOL BANAYA………..HAHAHAHA :tongue: :tongue: :tongue: :tongue: :yelo: :yelo: :yelo:
hi rati…. kiimii… farha….jomol….rads….nids….siree…. how r u all doing… ???
:toothygrin: :toothygrin: :toothygrin: :toothygrin: :toothygrin:
Nooooooooooppppppppppppoooooorrrrrrrrrrrrrrr hieeeeeeeeee :toothygrin: :toothygrin: :toothygrin: :toothygrin: :toothygrin: :toothygrin: :toothygrin: :toothygrin: :toothygrin: and wish Jomo :toothygrin:
Hey Noopur!!! Where were you itne din se? And how are you??????????? 😀 😀 😀
kimi kimi kiimi…
:happydance: :happydance: :happydance: :happydance: :happydance:
m much better now…. went out yesterday after a whole long month of house arrest….
khoobb shopping ki.. mjaaaaaa aaayaaa…
hows u??? 😀 😀
Shopping?????????????? Awessome!! :happydance: :happydance: :happydance: :happydance: Me want to see…I am good too..boss going to Germany for 2 weeks so me :happydance: :happydance: :happydance: :happydance: 😛 😛 😛
kimi…. hve u handed over a loong listt to the boss for things he can get u from germany :toothygrin: :toothygrin: :toothygrin: :toothygrin: :toothygrin: :toothygrin: :toothygrin:
Shopppinngggg????? Show show show!!! :waiting: :waiting: :waiting: :waiting:
Noopur…..you mujhe bhool gayi…. :((
No hi to me :(( :(( :((
aajkal sab meko ignoring :wilt: :wilt: :wilt: :wilt:
Ok….admit…I need some attention :toothygrin: :toothygrin: :toothygrin: :toothygrin:
jinal ji…. apko yahan alag se hi kehna padega???????????????????????????????????
:evilgrin: :toothygrin: :toothygrin: :toothygrin: :toothygrin: :toothygrin: :toothygrin: :toothygrin: :toothygrin: :toothygrin: :toothygrin: :toothygrin: :toothygrin:
main me got aldo se footwear… :victory2: :victory2:
n bagzz n perfume n lip pip n lifestyle se summery t shirts… :happydance: :happydance: :happydance: :happydance: :happydance: :happydance:
😯 😯 😯 😯 😯 :spank: :spank: :spank: :spank: :spank: :spank: :spank: :spank: :spank: :spank: so much shoppping :hunterwali: :hunterwali:
yes Noopur….me also want some attention :smug: :smug: :smug:
And you got so much………now u flaunt :hunterwali: :hunterwali: :hunterwali: :hunterwali: :hunterwali:
:toothygrin: :toothygrin: :toothygrin: :toothygrin: :toothygrin: :toothygrin: :toothygrin: :toothygrin: :toothygrin: :toothygrin: :toothygrin: :toothygrin: :toothygrin: :toothygrin: :toothygrin: :toothygrin: :toothygrin:
nhi laga nhi laga… :tongue: :tongue: :tongue: :tongue: :tongue: :tongue: :tongue: :tongue: :tongue:
abhi bol do….nahi laga nahi laga…..Delhi aaungi tab bohot lagegi :toothygrin: :toothygrin:
phir bachkar kahan jaogi :vampire: :vampire: :vampire:
u r comming delhi kya??????????when?………….. ?:)
yes sim….I will be there for 20 days…will reach on 21st morning :))
Hiiiiiiiiiiiiiiiiiiii noopurrrrrrrrrr……………… 😀 😀 😀
welcome jinal to our dehi……………. :toothygrin:
You’re looking lovely Mrunmayee 🙂
Thanks a lot Ankita!! :thanks: :thanks: :-* :-*
Thanks Ginni!!! Your comment made MY day!!! :thanks: :thanks: :thanks:
Mrun…………. :heart: :heart: :heart: :heart: :heart: :heart: :heart: :inlove: :inlove: :inlove: :inlove: :inlove: :inlove: :inlove: :inlove: :rose: :rose: :rose: :rose: :rose: :rose: :rose: :rose: :kissing: :kissing: :kissing: :kissing: :kissing: :kissing: :kissing: :kissing: :kissing: :kissing: :kissing: :kissing:
No words…..speechless :yahoo: :yahoo: :yahoo: :yahoo: :yahoo: :yahoo:
Jinalllllllllllllllllllllllll….
haaaan jeeeeeeeeeeeeee……….. 😀
Thank you Jinal!!!! :-* :-* :-* :-* :-* :thanks: :thanks: :thanks:
ki haal chaal? I suddenly feel like meeting you!!!
Kimiiiiiiii………..me toooooooooo :hugleft: :hugleft: :hugleft: :hugleft: :hugleft: :hugleft: :hugleft: :wilt: :wilt: :wilt: :wilt: :wilt: :wilt:
I wish we were in same city :weep: :weep: :weep: :weep:
yeah……I wish I had Doraemon’s magical door!! 😛
yeah….. 😛 😛
If I had it then I wud visit every city roz roz and meet and shop with all :victory2: :victory2: :victory2: :victory2:
he he he..just the thought itself is soo exciting naa!! :happydance: :happydance: :happydance: :happydance: :happydance: :happydance:
hai na :happydance: :happydance: :happydance: :happydance: :happydance: :happydance: :happydance: :happydance:
you and hubby come to Delhi na for holiday between 21st Apr-9th May…..we all have grand meet there :victory2: :victory2: :victory2: :victory2: :victory2: :victory2:
hmmm…such a tempting offer..we toh didn’t go for honeymoon too..was planning to go to Ooty this long weekend, but hubby spoiled the plan by all nakhraas..Aaj subah saasu maa scolded him and sasur jee asked him, when should he get our rooms booked at Ooty guesthouse, tab thodi akal aayi hai..Now he is urging me to go this weekend..I said, we’d go during good friday weekend now..iss weekend aaraam karo!! 😛 😛 😛
ahahaha……uffff ladko ke hazar nakhre…..aur hume nakhrewali kehte hai O:) O:) O:) O:)
ab aap thoda tadpao…tab akal aayegi hubby ko :toothygrin: :toothygrin:
But then have a great time there…. :victory2: :victory2: :victory2: :victory2:
Aur chupke se mujhe batana vahan kitne mazey kiye :secret2: :secret2: :secret2: :jiggy1: :jiggy1: :jiggy1: :jiggy1: O:) O:) O:) O:)
he hehe :toothygrin: sure!! :-* :-* :-* :-* :-*
Beautiful mrun :))
Kiiiiiiiiiiiiiiiiiiiiii!!!!! Where have you been???? i missssed you soooooooooooo much!!!! :happydance: :happydance: :happydance: :happydance: :happydance: :happydance: :happydance: :happydance: :happydance: :happydance: :happydance: :happydance: :happydance: :happydance: :happydance: :happydance: :happydance: :happydance: :happydance:
me missed you too!!!! :* so busy setting up a new home in a new place!!! ooh your wedding is coming 😀 😀 😀
finished wid all the entry post n so now luking at ur beauty,mrun :beauty: :beauty: :beauty: :beauty: .. luv ur hairdo :yahoo: :yahoo: … i wud try to do the french braid but i kno i’ll not b able to do it properly… 😐 😐 😐 😛 😛 😛 😛
This is a messy one na Nids, so try it!! me too can’t french braid very neatly.. And :thanks: :thanks: :thanks: :thanks: :thanks: :thanks: !!!
aree haan.. this is messy 1 & i can create a lot of messs….. :toothygrin: :toothygrin: :toothygrin: :toothygrin: :toothygrin: :toothygrin:
See???? :yahoo: :yahoo: :yahoo: :yahoo:
So easy! And I got a green glimmerstick by acon yesterday…. :yahoo: :yahoo: :yahoo: :yahoo:
me copycat this too….
ur messy bun looks so good… i wish i could carry looks like that….
Thanks a lot Anks!!!!! Please copy cat this and you toh would carry buns so well!!! Nice oval face you have!!!
mrunnnnn meri jaannn .. u make everything look so easy peasy … me will try .. but no e/s i have.. ek bhi nahin.. and now i regret not picking up maybelline quads :weep: :weep: :weep: :weep: :weep: :weep: :weep:
mruuunnnnnnn … i loveeeeeeee your confidence more than anything else :eat:
Thanks a lot Sweetie!!!! Maybelline quad toh you can get anytime na.. Easily available.. Get this brown one.. Very versatile!!!
And thanks a lot for the lovely comments!!! :-* :-* :-* :-* :-* :-* :-*
thats the whole beauty of the place i stay in ….. no maybelline .. now, how awesome is that :spank: :spank: :spank: :spank: :spank: :spank: :spank: :spank: :spank: :spank: :spank: :spank: :spank: :spank:
Where do you live Naina??? Do you have Westside or Pantaloons???? Maybelline is available at both the places.. I always thought I was the only one who couldn’t find stuff!!! ?:) ?:) ?:) ?:)
bhubaneswar ..pantaloons hai but no maybelline , no faces and no ‘all good brands’ :weep: :weep: :weep: :weep:
naina I think faces would come. It is their in house brand :toothygrin:
super pretty mrun !!! n d hairstyle is awesummm :inlove: :inlove:
I always mess up :((
you have lost weight kya??
Even I felt that…her face is looking thinner and features sharper!! 😛 😛
She has…. she told me she lost some 8 odd kilos, i think…. 🙂 shaadi ki preparation!
8 Kilos!!!! 😯 😯 😯 😯 😯 😯 😯 😯 😯 😯 😯 😯 😯 😯 😯 😯 😯 😯 😯 😯 😯 😯 😯 😯 😯 😯 😯 😯 😯 😯 😯
hawww…8 kgs….thats a lot…..but its such a lovely feeling when u loose wtg…suddenly lot of clothes which u liked on others …u can fit in….Mrun…. :inlove: :inlove: :inlove: :inlove: :inlove: :inlove: :inlove: lovely eye work
YAY!!!! You all think i lost weight!!!! :happydance: :happydance: :happydance: :happydance: :happydance: :happydance: :happydance: :happydance:
How i wish I had lost some weight!!! But it’s 5 pounds not 8 kilos!!!! But thanks anyways!! Me toh :woot: :woot: :woot: now!!!!
Hi Mrunmayee
I was thinking about wearing green/ copper combo over the coming weekend but was clueless to pull it off…. and not sure how the combo would look on our Indian skin tone… and there you come with this look. Yout red lips rock with green/ copper eyes….
I think i have similar products and can recreate this look
Thank you so much …. :heart: :heart:
Hey Eesha!! Thanks a lot..
Please try this out and post piccys of the outcome!! :thanks: :thanks: :thanks:
my god Mrun..hw do u make such nice hair do..i toh pull up a pony or a bun..and race out….bus… 🙁
very prettty..nice lippie too 🙂
Thanks Zeeba.. Trust me.. I am the clumsiest person when it comes to hair!!! Braids and buns were invented to camouflage bad hair!!! :thanks: :thanks: :thanks: :thanks:
thnx mrun..m sooo happy :yahoo: :yahoo: …..tmrw m gng fr shoppng wil buy all d thngs u mentioned here..bt i hve revlon touch nd glow already..hvnt used it..bt i guess its similar to lakme invisible 1…all d oder prdcts…here i cme :woot: ….luv u mrun…u r bestest :-* :-* …ek bat btauu…yesterday..i bought a cheap blue heaven eyeliner jst to learn hw to use it..today i tried it..nd i did a decent job..nw i learn hw to use eyeliner. :yahoo: :yahoo: tmrw i ll buy maybelline gel liner..its gud na….. :yahoo: :aajanachle:
I am sooo happy that you lovved it Jigyasa.. It made the efforts worthwhile!!! :-* :-* :-* :-* :-* :-* :-*
i cudn’t wait to try d hair do..i did it instantly..nd its lukng jst woooowwww…luv u mrun fr dese easy nd sensational hairdo… :aajanachle: :dance: :clap:
Yay!!! :jiggy1: :jiggy1: :jiggy1: :jiggy1:
loved ur last pic… u r beautiful O:) O:) O:) O:) O:)
Thanks Sugisoni!!! :thanks: :thanks: :thanks: :thanks: :blush: :blush:
awesome yaa Mrun– very saaxxxyyy
btw- lippie kaunsa lagaya hain – it suits u so good 😀
hey O:) bee….
Thanks Bee!!!
The lippie is Colorbar “love that Rust”. :thanks: :thanks:
u looking soo nice in that lipclour mrun..!! u totaly rocking it!! i loveeeeeed the last hair styleee :woot: :woot: :woot:
Thanks a lot Neha!!! :yahoo: :yahoo:
d last pic is hot….. luvd d hairstyle.
Thanks manali!!! Do try it out!! :thanks: :thanks: :thanks:
You looking hot, hot, hot, Mrun. I must try this look tomorrow itself. :)) :)) :yahoo:
Awww… Thanks Sabrina!! I am sure you will rock this!!! :thanks: :thanks: :yahoo: :yahoo: :yahoo: