The Body Shop Body Butter Duo Vanilla Review

Claims : The Body Shop understands that certain parts of the body, such as elbows and knees, have fewer sebaceous glands and therefore need more intense moisture to keep skin looking and feeling at its optimum. This is highlighted by the 72% of women who claim to have areas of very dry skin, necessitating the use of multiple lotions and potions to keep skin soft and moisturised. Body Butter Duo now makes your life easier. One product, two formulations, sharing the same fragrance – simply divided by smart packaging. Apply the rich infusion on areas such as elbows,knees, and legs, and use the normal skin formula on the rest of your body, for up to 24-hours of moisturisation.
Price : Rs 845 for 200 ml

Ida has already done a detailed review on the Body Butter Duo Macadamia HERE. So I’d quickly run you through the likes and dislikes about the vanilla variant of the body butter duo.
Ingredients:
Likes and dislikes :
- Super excellent concept and honestly, it works. I have been using it for almost a month now and I can already feel that my knees and elbows are softer than before. Also, I feel the vanilla variant is great for normal to dry skin types. In fact, both the products are so moisturizing that I don’t feel dryness until the next day.
- The lighter part of the cream is meant for the body . It is light in texture and gets absorbed easily in skin. The thick cream part of the duo is a bit heavier and thicker. You need to rub it a bit for it to get completely absorbed.
- The biggest turn off of the vanilla body butter duo is the fragrance. First, it feels a little artificial and second it is super strong for my liking. It smells like strong warm scented vanilla. The cream part has much stronger fragrance than the lotion part. The fragrance is so-so-so strong that it stays until the next day. I totally dread the usage of it if in morning I have to meet someone that day because this could just be too over whelming for the other person.
- The other drawback I feel is that the light cream part would finish up much faster than the thick cream part. In that case, you could probably fill up the empty part with your regular lotion or cream to make it convenient for you.
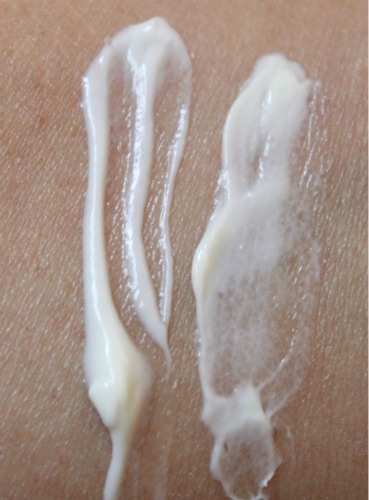
Swatch : Left – light cream meant for body, right- thicker cream meant for knees, elbows etc.
Overall , I loved the moisturizing part and the whole concept but I don’t think I would be purchasing the vanilla variant again. I would however suggest you that before purchasing you apply it on your hand/ arm, smell it and then decide. Some of you might actually like it. Product wise, it’s excellent.
I’d go with two ratings this time :
Product 4/5
Fragrance : 1.5/5
Have you used The Body Shop Body Butter Duo Vanilla ? Please rate in the box below
Chocolates Courtesy : Nupur. 😀
Also Read :
The Body Shop Body Butter Duo Macadamia Review
Shea Body Butter
Fabindia Almond and Coconut Body Butter
The Strawberry Body Butter, Raspberry Body Scrub, Clinique Anti Blemish
Lush Body Butter
Satsuma Body Butter and Soap
Japanese Cherry Blossom Body Butter
H2O Plus Sea Marine Triple Butter Cream
Wild honeysuckle BodyButter
The Body Shop BodyButter Duo Info
MAC Cham Pale Fix + Lavender, Lip Conditioner, Total Comfort Cream
ST.Ives Swiss Vanilla-Advanced Body Moisturizer
Khadi Herbal Hair Conditioner with Vanilla and Honey
Lotus Herbals Vanilla Lip Therapy
MAC Wonder Woman Pigment, Reflects Glitter, Mascara Photos, Swatches










Rati di! Kya fotografy hai! wallah wallah types :jaiho: And how I want to get this tub!! And I think I’ll like vanilla! 😀
try it out sukanya. it’s a great product. :))
excellent photography rati :inlove:
chocolates look so yummy…nufur- u made the chocos?
oh yeah vids, she is a chocolatier.. :))
thanks. 🙂
:drool: :drool: :drool: you’ve started clicking super tasty pics :drool: , first that maybelline one and now this! :pan:
I want those chocolates! :ghost2: :ghost2:
hihihihihi thankoo!!! :yahoo: :yahoo: :yahoo: :yahoo: :yahoo: :yahoo: :yahoo: :yahoo: :yahoo:
:yahoo: :yahoo: :yahoo: :yahoo: :yahoo: :yahoo: :yahoo: :yahoo: :yahoo: :yahoo: :yahoo: :yahoo: :yahoo:
:happydance: :happydance: :happydance: :happydance: :happydance: :happydance: :happydance:
nufurr i want the chocos :waaa: :waaa:
nufur bolne walon ko chocolates bilkul nhi milengi :vampire: :vampire:
:huh: :huh: :huh: :huh: :huh:
🙁 :(( :waaa:
aaj se nuuu bulaungi tumhe
:haanji: :haanji: :haanji: :haanji: :haanji: :haanji: :haanji:
i want some coffeee n chocolates abhi k abhi ryt nowwwww :waaa: :waaa: :waaa: :waaa: :waaa: :waaa:
you toh can have it too.. :huh: I just had coffeee :yahoo: :yahoo: :yahoo: :yahoo:
and yeh two-two creams in 1 wala TBS body butter bhi :worship: :worship: :worship: :worship: :worship: :worship:
check out the one that ida reviewed. I feel that has milder fragrance than this one.
these coffee beans na i churaaoed from one restaurant. We went to a friend’s happy buddy party. so the waiter got the bill in a mug with loads of coffee beans.. I took all the coffee beans. :jiggy1: :jiggy1: :jiggy1:
haaawwww….. :toothygrin: :toothygrin: :toothygrin: :toothygrin:
u followinggg crime master gogo… aayaaa hun toh kuch le k hi jaaunga :toothygrin: :toothygrin: :toothygrin: :toothygrin: :toothygrin: :toothygrin: :toothygrin:
Nupuriiiiiiiiiiiiiiii :lol2: :lol2: :lol2: :lol2: :lol2: :lol2: :lol2: :lol2: :lol2: :lol2: :lol2:
imagined what the waiter might have thought….”bechari….kitni bhooki thi…..coffee beans bhi nahin baaki rakha” :methinks: :methinks: :methinks: :methinks: :methinks: :methinks: :methinks: :methinks: :methinks: :methinks: :methinks: :methinks: :methinks: :methinks: :methinks: :methinks:
:lol2: :lol2: :lol2: :lol2: :lol2: sachhi.. waiter n yehich soha hoga :teeth :teeth :teeth :teeth
:hunterwali: :hunterwali: :hunterwali: :hunterwali: :hunterwali: :hunterwali: :hunterwali: :hunterwali:
:dumb: :dumb: :dumb:
jomo, m very ishmaartttt…. i churaaofy useful items like saunfff from restaurants… no coffeee beans :victory2: :victory2: :victory2: :vampire: :vampire: :vampire: :vampire:
Main bhi Nupurrrrrrrrrrrrrrrrrrrrrrrrrrrriiiiiiiiiiiiiii….I also pick up extra saunf :happydance: :happydance: :happydance: :happydance: :happydance: :happydance: :happydance: :happydance: :happydance: :happydance: :happydance: :happydance: :handshake: :handshake: :handshake: :handshake: :handshake: :handshake: :handshake:
yeah right churaaoing coffe beans is a bigger crime than churaaoing coffe beans ?? :hunterwali: :hunterwali: :hunterwali: :hunterwali: :hunterwali: :hunterwali:
coffee beans tho we don’t steal Rati…its so bitter to eat….we tho pick up saunf only :shy: :shy: :shy: :shy: :shy: :shy: :shy: :shy:
Nupur, mint flavour wali??? :toothygrin: :toothygrin:
😆 😆 😆
O:) O:) O:) O:) O:) O:) O:)
I love your photos Rati……………..and the body shop duo :jaiho: :jaiho: :jaiho: :jaiho: :jaiho: :jaiho: :jaiho: :jaiho: :jaiho: :jaiho: :jaiho: :jaiho:
thankoo jomol :yahoo: :yahoo: :yahoo: :yahoo: :yahoo:
You are using the tips I gave you about photography very nicely….I am happy with you….. :haanji: :haanji: :haanji: :haanji: :haanji: :haanji: :haanji: :haanji:
yes but i still cant take the signature pic as bootifully as you do :vampire: :vampire: :vampire: :vampire:
you stole coffee beans :spank: :spank: :spank: :spank: :spank: :spank: :spank: :spank: :spank:
you dont see my dedication :smug: :smug: :smug: :smug: :smug: :smug: :smug: :smug:
what is your nearest police chauki’s name :spank: :spank: :spank: :spank: :spank: :spank:
Secunderabad Police station.
Criminal Name – jomol J
O:) O:)
Amazing photographs Rati. The body butter looks so yummy :woot: :woot: :woot:
thanks Jyoo!! :yahoo: :yahoo: :yahoo: :yahoo:
:spank: :spank: :spank: this is for u nupur. For making such yummy looking chocies n not sending thm wid my package :smug: :smug: :smug:
jaaan le lo bache k sabb :spank: :spank: :spank: :spank: :spank: :spank: :spank:
Nupurrrrrrrrrrrrrrrrrrrrrrrri……………nupurrrrrrrrrrrrrrrrrrrrrrriiiiiiiiii badnaam hui…..handmade chocolate ke liye :woot: :woot: :woot: :woot: :woot: :woot: :woot:
:toothygrin: :toothygrin: :toothygrin:
the words butter n vanilla are making my mouth water…n so is the photography… :drool: :drool: :drool: :drool: :drool: :drool: :drool:
i don’t mind strong scents (especially vanilla) but it’ll be wise to check before buying something so expensive i guess.. :haanji: :haanji: :haanji:
oh do check it out tinkerbell. i got deluded by the same words :stars: :stars: :stars: :stars: :stars:
:preen: :preen: :preen: What an idea! Now even I waaaaaannnnttt!! :waaa: :waaa: :waaa: :waaa:
Nupur di…I’m so J of you! :green: Always surrounded by chocolates…plain cocoa,almonds,hazelnuts,fruit and nut….My mouth is watering! :drool: :drool:
Aur ye Rati ek…always thoosing your chocies. :huh: :huh: :huh: :hunterwali:
…Now the concept of a box of chocolates with a cup of cold coffee is just too tempting! :love:
Abhi jakar le ati hu. :jog: :dumb:
thoosooingg? :spank: :spank: :spank: :spank: :spank: :spank: :spank: :spank: :spank: :spank: :spank: :preen: :preen: :preen: :preen:
Yes…Jab dekho,”Nupur ki chocies! Nupur ki chocies!” karti rahti ho. :huh: :huh: :huh:
:hunterwali: :hunterwali:
I am lucky :huh:
:bash: That was what I’ve been saying up till now… 😥
am drooling :drool: … i cant agree more with u pragnyadeepta :haanji:
Pragnyyyyyyyyyy…mekko bhi chahiye :waaa: :waaa: :waaa: :waaa: :waaa:
O:) O:) O:)
Jomol…I feel your pain. 😥 😥
Is Rati ko toh… :bash: :bash:
pragny,,,,,,,,,,,,,,,, 😥 😥 😥 😥 😥 😥 😥 😥 😥 😥
Rati, I have this one in floral acai.. It has a very mild floral fragrance that actually disappears after a while. At first I was a little disappointed by that, but I think now that its probably good that way. As u say, strong fragrances can be a put-off.
Totally loving ur creative pics!! :yes: :yes: :yes:
thanks ramya. I tried that at the store afte few days of purchasing this. i liked the mild fragrance of it. :))
Yes, its a very delicate kinda fragrance, if that makes any sense. I like it. Maybe u could pick that next time! 🙂
I’ll do that because I love the product itself. 🙂
Hai na?? Such an innovative concept! I toh wondering if I can go back to the regular butters after this 🙂
same here. I dnt want to go back to normal body butters any more. 😀 😀
:haanji: :haanji:
i am quickly finishing the existing body butters so that i can buy thiss :toothygrin: :toothygrin: :toothygrin:
i was thinking about your yesterday pereeya.. .. 😀 howz you doingz? 😀
Priyyyyyyyyyyyyyyyyyya :happydance: :happydance: :happydance: :happydance: :happydance: :happydance: :happydance:
i want 1 of these but abhi 1 more mnth can go without it… :haanji: :haanji: :haanji: :haanji: n yesss rati.. gr8 photugraphy :pompom: :pompom: .. ahkal chocos bahut dikh rhi hai tumhari pics mei.. lagta hai khane ki jagah sirf photus kheenchne ke liye hi rakhi hai tumne ye chocos.. tabhi u loosing weight na,.. :methinks: :haanji:
oh yeahh!! 😀 😀
the chocies are almost over :shame: :shame: :shame: :shame: :shame:
I love vanilla fragrance a lot ! 😀 So I may like it !! I want to try this range !! when will go to kolkata will surely buy this one !
hope you like it. :))
hey hi have any buddy ever used orifalme scruber how is it ?
Ratii…agli bar Nupur di se chocies milenge na..toh don’t use them in photos of makeup…instead take few of them and put them in a box and lock it…then work your bt off until you really feel like you deserve a treat…the thoosofy them. O:) O:)
This way thoda weight bhi ghat jayega,and yo can eat chocies too…. :jalwa: :jalwa:
Sorry Jomol di…I know you are thinking ki “ye ladki kaikoo advicing?? Yedi hai kya? ”
…That is a secret ok. :secret2:
O:)
i think you hve really gone yedi today. :lol2: :lol2: :lol2: :lol2: :lol2: :lol2: :lol2: :lol2:
Pragnyyyyyyyyyyyy :haanji: :haanji: :haanji: :haanji: :haanji: :haanji: :haanji: I understand dear…..hamari ek hi pareshani hai :haanji: :mirror:
Rati…I agree with the strong smell part…I have vanilla too and I totally dislike the smell. :spank: :spank:
Once I’m done I’ll fill it up with 2 of my fav lotions :yahoo: :yahoo:
same here :yahoo: :yahoo: :yahoo: :yahoo: :yahoo: which are your fav lotions? 🙂
Wild Cherry & Strawberry from TBS….sometimes I feel the need for Nivea too 🙂
This looks quite good Rati..and me love strong fragrances!! 😀
oh then you must give this a try. 🙂
hi rati..thnx for the review :thanks:
ever since am hooked into imbb i have heard all of you going ga-ga over these body butters… n frankly i didnt have any idea about what it actually does and how to use :shame: :shame: … though the names used tp tempt me a lot :stars:
strong smell is not much of an issue to me,vanilla too is one of my fav flavour….and woowie its good for dry skin too :yahoo: :yahoo: :yahoo: ……..am really really excited to try this out :haanji: … just waiting for tha tbs sale to come again……… O:)
that would be in jan end i guess. tab tak toh you wouldnt even need body butters… 😛 But they keep having member’s sale so that you may keep an eye on. :))
member’s sale??? how to become member??? sorry am totally novice regarding beauty updates… n imbb is my only rescuer :shame: :shame:
you just pay Rs 500 and become a member :yahoo: :yahoo: :yahoo: :yahoo: :yahoo: :yahoo: :yahoo: :yahoo: :yahoo:
hein have to pay to become member? i toh became member directly without paying ony. dnt even remember how… by the way m i a member ther? now me think.. i do get promotional msgs of tbs almost every week :waaa:
u got freeee !!!!!!!!!!! :green: :green: :green: :green: :smug: :smug: :smug:
thanx rati…
I think they send alerts to everyone, sugi O:) O:)
Chociesssssssssssssssssssss….what a show off :spank: :spank: :spank: :spank: :spank: :spank: :spank: :spank: :smug: :smug: :smug: :smug: :smug:
oh! I forgot to tell you that we had blooberry french cheese cake.. i forgot the blooberry part you see. :preen: :preen: :preen:
I hope you stay in the bathroom area for a long long time :spank: :spank: :spank: :spank: :spank: :spank: :spank: :spank: :spank:
i collect cans for you there :sick: :sick: :sick: :sick: :sick: :sick: :sick:
:jaiho: :jaiho: :jaiho: :jaiho: :jaiho: cudnt take my eyes off the pictures……. u r doing a wonderful job Rati, This is one of ur best photography’s….
thanks shivani. 🙂
but looks yumm..sad that the fragrance is not so good 🙁
good review and awesome photographs, Rati 🙂
thanks praseena. 🙂
Bhumika , yeah am not a huge fan of the fragrance. 🙁
Ratiiiiiiiiiiiiiiiiiii
:jaiho: :jaiho: :jaiho:
Maybe you should start photo-blogging as well :methinks: :methinks:
thanks mansi.. :)) I hope i continue photoblogging on imbb only. 😀 😀
lovely review. can body butter be used for face as a night cream
(for dry and sensitive skin)
chandana, it is meant mainly for body so i never tried it on face. and dont recommend you to do so as well.
such an amazing concept!! I really need to get this for my dry skin. (just hands and feet 😛 )
Will try different variant thought.
Abhi last week they had 20% off specially for members…..I missed it :((
it’s really good jinal. 🙂 You should give it a shot! 🙂
I am also planning to take membership. I have started buying quite a lot of TBS stuff. 😀
nice photography rati 🙂 …. have used this one and i agree bout the smell part.. its pretty strong…but i just fell in love wid the whole concept of this duo..so will buy again mayb a different one this time… 😉
thanks robbie. 🙂 same here. i would def purchase the different variant in this one. :))
this looks nice…although quite expensive…hmmmnnnn will hv to test the fragrance tab pata chalega ki lena chahiye ya nahi…i dont like strong ones either :waiting:
yeah definitely try the fragrance bhawana. this is like too strong for my liking. :((
Hi Rati , Link to Body Butter Duo Macadamia is not working.. :methinks: :methinks:
seems quite a promising product Rati!!! but me too cant take strong fragrance :yikes: :yikes: Delhi mein toh thoda thoda winters shuru ho gaya hga na sighhhhhhhhh
expensiveeee…bt I luv vanilla smell… :rotfl:
Nice review :waytogo: . i wish I had read this before buying the product. The smell is too powerful and not much to my liking.