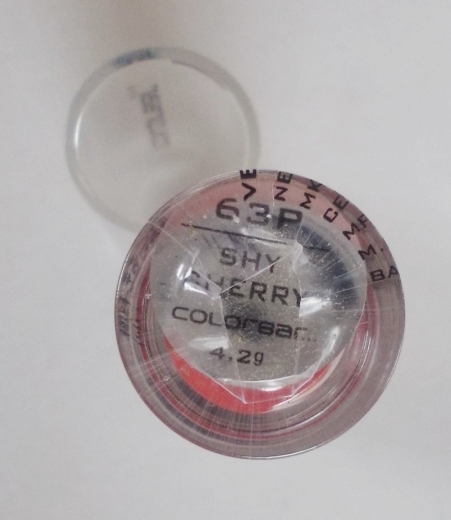
Colorbar Velvet Matte Lipstick: Shy Cherry Review
I am very excited to write this review now. After ages, I have found a Colorbar Velvet Matte Lipstick that does not stain a hot pink! I could not believe my eyes when I saw what this lipstick delivered and I am happily recommending this lipstick that made my week.

For the first time, I am not cribbing about the new formula of these Colorbar velvet matte lipsticks. I picked this one up from Pune and I picked up three shades randomly. I know I say these stain and dry, but still, when I swatch these lipsticks, the colours are so tempting and the pigmentation is through the roof that its hard to resist and then I always think I will review them if not use them.

The lipstick comes as a surprise to me. I was eyeing this lipstick since Rati shared the six new shades, but when I realized these stain inevitably, I gave it up. I bought Thrilling Pink and a couple of others, but when I swatched this one, I was floored. This is the exact color I can wear for the next one decade because I absolutely love carroty pinky reds.
I don’t know how to define this shade, it’s a reddish carrot pink color. The texture is hard but when you swipe it, you get a very deep pigmented thick stroke of color. That is what surprises me a lot. The lipstick feel hard and sturdy in the tube but when you glide it across, it feels quite smooth as in not delicate and melting smooth, but firm yet smooth :p I hope you get what I mean.
The pigmentation is amazing on this one, very deep, thick and creamy. It is not exactly matte, but it has a moisture sheen to it. I won’t say it is not drying. I do feel after some time, my lips tend to get dry with Colorbar Velvet Matte’s new formula.
The best part is that this lipstick won’t stain like the others from Colorbar Velvet Matte range. The lipstick is so red and deep, but still, it won’t leave the horrid hot pink stain and hence I am happy at this discovery, maybe Colorbar has woken up to change the staining formula.
The staying power is very good too. Without meals, it will last for 4 hours easily on me. I do need a lip liner with this and to tone it down, one can use a lip brush too. I have applied the lipstick with a Lakme lip brush in the swatch. The only downside of this one is that maybe after some time it stays on you lips, you may find it drying and irritating.
Last Word:
Great color for 250 rupees, deep pigmented texture, won’t stain and lasts long. Can be a little dry after some time though. I am recommending this velvet matte lipstick to everyone after a long time.
IMBB Rating:
4.5/5
Colorbar Velvet Matte Lipstick Thrilling Pink
Colorbar Velvet Matte Lipstick Pure Innocence
Colorbar Velvet Matte Lipstick in Peach Crush
Colorbar Velvet Matte Lipstick Over The Top 1
Colorbar Velvet Matte Lipstick Crème Cup
Colorbar Velvet Matte Lipstick Peach Tango 09P
Colorbar Velvet Matte Lipstick Iced Tea
10 Most Favourite Colorbar Matte Lipsticks
Revlon Colorburst Lipstick- Peach
Estee Lauder Pure Color Long Lasting Lipstick Sugar Honey Review, Swatches
Chanel Rouge Allure Lipstick Genial
Chanel Rouge Coco Lipstick
Colorbar Velvet Matte Lipstick in Bare
L’Oreal Glam Shine 6 Hours Lip Gloss Purple Obsession, Blush Mania
MAC Optimistic Orange Cremeblend Blush
Chambor Powder Matte Lipstick: Orange Flambe
MAC Kid Orange Nail Polish Photos, Swatches
Colorbar Velvet Matte Lipstick – Obsessed Orange






![Sandwiches_for_weight_loss[1]](https://makeupandbeauty.com/wp-content/uploads/2024/04/Sandwiches_for_weight_loss1.jpg)






where is the most famous LOTD!????????????i first saw ur LOTD den go back n read d review….
arey i had sent it
got miss i think
Me too parvi…
well the shade is lookin awesome!!!!!
yes 🙂
LOTD? I am a fan of ur lips… Errrrr… Lol
had sent it lemme check with jOmol 🙂
that’s a gogrrgoeus color neha. i agree. I am also missing your lip swatch. 🙂
i had sent the swatch plz 🙂
missed out?
the color is very pretty but me wanna see the lip swatch 🙂
:p had sent it (again)
Very pretty shade Neha! Lippie reviews are soooo not complete without your mind blowing lip swatches! Waiting for your lip swatch now 🙂
Jomol jomol jomol please cud u post the lip swatch 🙂
thnks aarbee
Gorgeous color Neha…. 🙂 as usual u find the best shades in the market 😉
Thanks
hahah thnks nats 🙂
Great shade neha..
I loved the color..
Neha this is so unfair.. me wants to see your lip swatch 🙁 🙁 🙁
Finally u found one which does not stain pink :p Shade looks nice..
Lip swatch lip swatch! Humari maange poori karo! 😀
Yay!
the lip swatch is HERE 😀
Lovely lip swatch <3 🙂
OMG … ur lips …. droooollllllllllllllllllllllllllllllllllll… gorgeous this shade is looking on u neha… ur lip swatch is tempting me to try this lippie.. tho otherwise i probably never wud.. :p im super scared of wearing red n hot pink lippies somehow.. 🙁
lovely colour 😀
Loved the shade…. and ur lips look delicious 😉
Wow Neha you finally hit the right colorbar stick! So happy for you! But quite confused with the shade, carotty pinky red ? I am not sure how good it would look and on whaetish skin color! But glad it worked for you!!!!!!!!!!!!!!!!!!!
nice color 🙂
i wish i had picked up this one instead of Thrilling pink, that stains majorly man!!! 🙁 neha cud u suggest a dupe of thrilling pink, that colour is gorgeous but it stains n turns fuschia pink in some time….sobsob
bful shade….looks gr88 on u ..